W niniejszym wpisie umieściłem część materiału związane z prezentacją i pochodzeniem wybranych miar binarnych. Prezentowane treści ze względu na ograniczone możliwości redakcyjne musiały zostać usunięte z niektórych publikacji. Niemniej blog nie ma żadnych ograniczeń tak więc zachęcam do zapoznania się z pochodzeniem i z odmianami niektórych miar binarnych oraz z autorskimi wyprowadzeniami niektórych z nich.
1. Wstęp
Przy założeniu, że dokumenty są indeksowane binarnie tj. do dyspozycji jest binarny wektor wyrażeń, zawierający wagi wyrażeń opisujących dany dokument d. Waga wyrażenia w tej reprezentacji przyjmuje wartość 0 – wyrażenie t nie występuje w dokumencie d lub 1– wyrażenie t występuje w dokumencie d. W celu odnalezienia dystansu lub podobieństwa pomiędzy samymi przypadkami zdarzeń (dokumentami tekstowymi) jak i pomiędzy przypadkami zdarzeń a zapytaniem Q, należy posłużyć się jedną z 76 dostępnych miar binarnych opisanych m.in. w pracach [1-3]. Zapytanie Q traktowane jest jako zredukowany opis przypadku do kilku znaczących wyrażeń t podawanych przez Kierującego Działaniami Ratowniczymi KDR w celu wyszukania na ich podstawie najlepiej pasujących przypadków z bazy wiedzy systemu CBR. Miary binarne powstały na początku XX wieku, a ich rozwój zaczął się od zaproponowanej w 1901 przez Jacarda miary podobieństwa gatunków. Miary te są szczególnym przypadkiem miar stosowanych do pomiaru dystansu, podobieństwa pomiędzy wektorami nie binarnymi, czyli takimi których wagi mogą przybierać wartości nie tylko 0 lub 1. Przegląd i zastosowania miar nie binarnych można odnaleźć m.in. w pracach [4, 5].
W tej części artykułu autor skoncentrował się na przedstawieniu probabilistycznej genezy drugiej miary Kulczyńskiego (Kulczyński II) ze względu na to, że w różnych publikacjach pomijany jest fakt skąd ta miara się wywodzi. Autor przedstawił także probabilistyczne pochodzenie miary Gilberta i Wellsa. Dodatkowo dla tej miary autor przedstawili wariację na temat zabezpieczania algorytmu wykorzystującego tą miarę przed występowaniem logarytmu z zera. W dalszej kolejności przedstawiono wersję binarną znormalizowanej informacji wzajemnej mającej także podstawy probabilistyczne [5]. Wersja ta nie była dotychczas przytaczana w żadnej literaturze znanej autorowi. Na koniec punktu dotyczącego miar autor odstąpił od ścisłego proponowania miar opartych o probabilistykę i zaprezentowali uogólnione podejście do reprezentowania miar Ostuka i Ochiai, Barun i Banquest oraz Simpsona na podstawie miary Ochiai II. Równania określające podobieństwo dokumentów wyróżnione symbolem (*) oznaczają, że autor nie znalazł ich omówień w dostępnej dla niego literaturze z zakresu miar binarnych.
Do dalszych rozważań przyjęto następującą notację [5]:
– x – oznacza dokument reprezentowany za pomocą wektora wyrażeń zawierającego ich wagi
– y – oznacza dokument reprezentowany za pomocą wektora wyrażeń zawierającego ich wagi
– S(x,y) – oznacza miarę podobieństwa (ang. similarity) pomiędzy dokumentami x i y
– P(x|y) – oznacza prawdopodobieństwo warunkowe zajścia zdarzenia x pod warunkiem zajścia zdarzenia y
– dfxy – oznacza liczbę wspólnych wyrażeń dokumentów x i y
– dfx – oznacza liczbę wyrażeń w dokumencie x
– dfy – oznacza liczbę wyrażeń w dokumencie y
W miarach binarnych najczęściej stosowana jest notacja a, b, c, d, n,
gdzie [1]:
– a – odpowiada ilościom pozytywnych dopasowań wyrażonego schematem 11 tj. wyrażenie na i-tej pozycji wektora wyrażeń dokumentu x przyjmuje wartość 1 natomiast dla tej samej pozycji dokumentu y wartość ta wynosi też 1
– b – odpowiada ilości dopasowań według schematu 10 tj. wyrażenie na i-tej pozycji wektora wyrażeń dokumentu x przyjmuje wartość 1 natomiast dla tej samej pozycji dokumentu y wartość ta wynosi 0
– c – odpowiada ilości dopasowań według schematu 01 tj. wyrażenie na i-tej pozycji wektora wyrażeń dokumentu x przyjmuje wartość 0 natomiast dla tej samej pozycji dokumentu y wartość ta wynosi 1
– d – odpowiada ilościom negatywnych dopasowań wyrażonego schematem 00 tj. wyrażenie na i-tej pozycji wektora wyrażeń dokumentu x przyjmuje wartość 0 natomiast dla tej samej pozycji dokumentu y wartość ta wynosi 0
– n – powstaje przez sumowanie ilości ww. kombinacji i wyrażana jest w postaci wzoru n=a+b+c+d.
Zależności między oznaczeniami dla miar ogólnych i binarnych prezentują się następująco: dfxy = a, dfx = a+b oraz dfy = b.
2. Miary wywodzące się z rachunku prawdopodobieństwa
Binarna miara – Kulczyński II
Binarną miarę Kulczyński II można otrzymać z średniego prawdopodobieństwa warunkowego (Równanie 1).
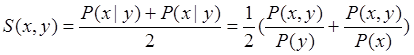 |
(1) |
Średnie prawdopodobieństwo warunkowe można oszacować za pomocą wzoru przedstawionego jako Równanie 2.
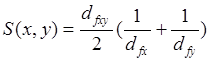 |
(2) |
Dokonując podstawienia i przekształceń algebraicznych otrzymana zostanie wersja binarna miary podobieństwa Kulczynski II, którą prezentuje Równanie 3.
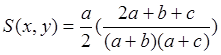 |
(3) |
Binarna miara – Gilberta i Wellsa
Binarną miarę Gilberta i Wellsa (Równanie 12) można otrzymać z informacji wzajemnej (Równanie 4).
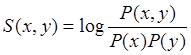 |
(4) |
Informację wzajemną można oszacować za pomocą wzoru przedstawionego jako Równanie 5.
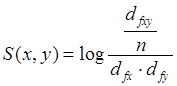 |
(5) |
Dokonując podstawienia i przekształceń algebraicznych otrzymana zostanie wersja binarna miary podobieństwa Gilberta i Wellsa, które prezentuje Równanie (Równanie 7).
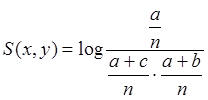 |
(6) |
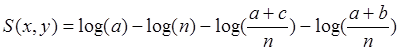 |
(7) |
W celu uniknięcia przypadku logarytmowania przez zero i otrzymania wartości nieokreślonej, można zastosować chwyt z odległości Lorentziana [4] tj. dodając 1 w wyrażeniach logarytmicznych.
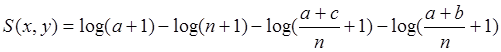 |
(8*) |
Binarna miara znormalizowanej informacji wzajemnej
Binarną miarę znormalizowanej informacji wzajemnej (Równanie 12) można otrzymać ze znormalizowanej informacji wzajemnej (Równanie 9).
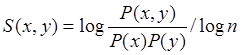 |
(9) |
Znormalizowaną informację wzajemną można oszacować za pomocą wzoru przedstawionego jako Równanie 10.
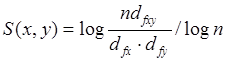 |
(10) |
Dokonując podstawienia i przekształceń algebraicznych otrzymana zostanie wersja binarna miary znormalizowanej informacji wzajemnej, którą prezentuje Równanie 12.
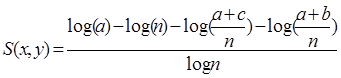 |
(11) |
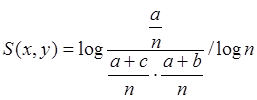 |
(12*) |
W celu uniknięcia przypadku logarytmowania przez zero i otrzymania wartości nieokreślonej, można zastosować chwyt z odległości Lorentziana [4] tj. dodając 1 w wyrażeniach logarytmicznych. Rezultat tego działania przedstawia Równanie 13.
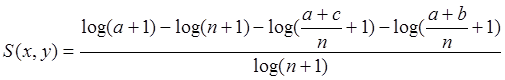 |
(13*) |
Binarna miara – Bayesa
Binarna miara podobieństwa dwóch wektorów binarnych bazująca na naiwnym twierdzeniu Bayesa może zostać wyrażona za pomocą Równania 14.
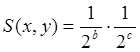 |
(14*) |
Literatura